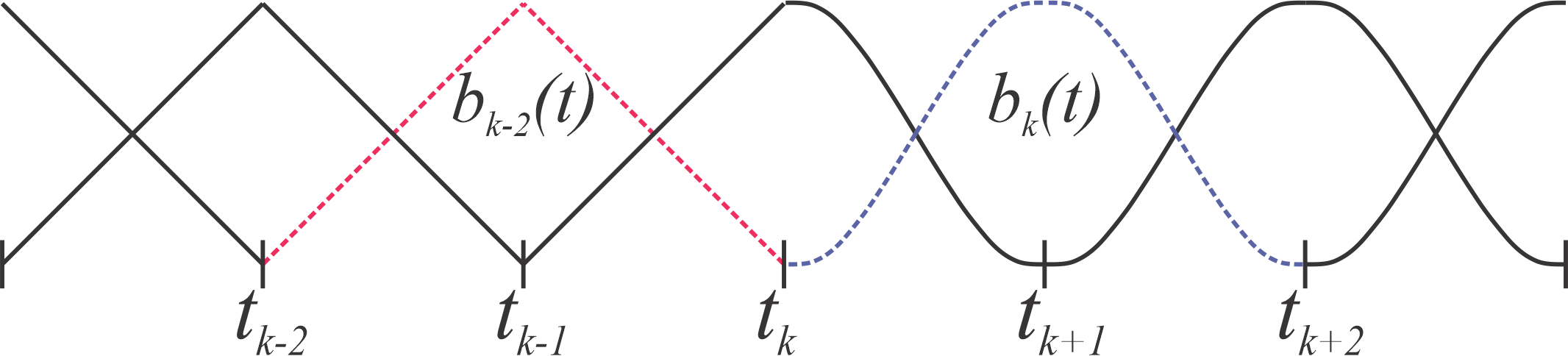
Blending-splines

              

Figure 8.4, an image of knots and basis-functions of a B-spline curve of degree 1, which then become basis-functions with B-functions on the right-hand side.

In the figure is \(b_{k-2}(t) = w_{1,k-2}(t)\)  when \(t\in [t_{k-2},  t_{k-1}) \)  and  \(b_{k}(t) = B\circ w_{1,k}(t)\)  when  \(t\in [t_{k},  t_{k+1}) \).  \(w_{d,i}(t) = \frac{t-t_i}{t_{i+d} - t_i}\).

A blending-spline curve is a 2nd order B-spline with the formula:  \( C(t) = \displaystyle\sum_{i=0}^{n-1} c_i(t)\ B \circ b_{1,i}(t),\ \ \) where we have \(n\) control curves \(c_i(t)\) and \(n\) scalar basis functions \(B \circ b_{d,i}(t)\). In the figure above, a set of basis functions is plotted, to the left ordinary 2nd order B-splines, and towards the right they change with B-functions. See chapter 8.2 in the book Blending techniques in Curve and Surface constructions.

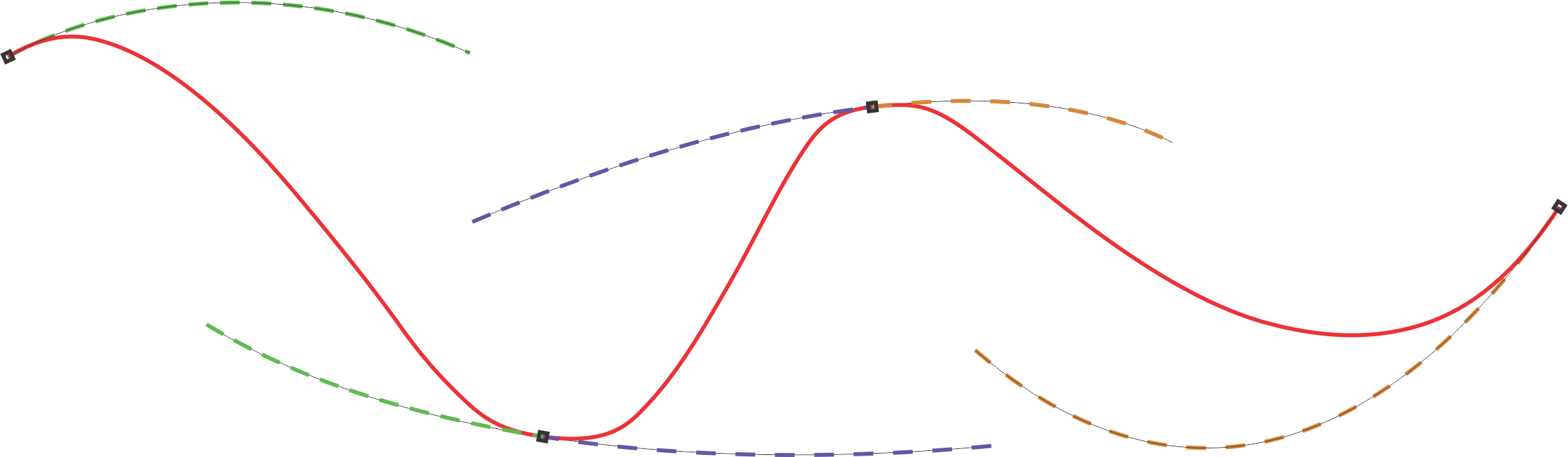
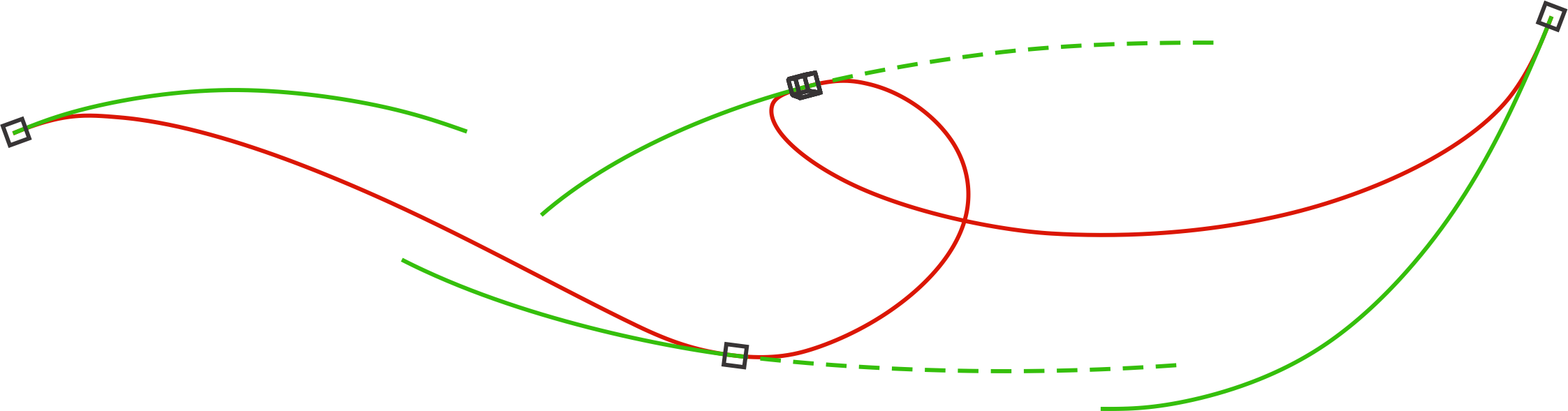
In the figures below we see blending-spline curves. On the left we see a curve which is a blending of 4 local (control) curves. On the right, the same curve has been changed in that tree of the local curves have been moved and two of them have been rotated.

     

If you click on the figures, you will get a blending-splines where you can make changes graphically.

The figures is from Figure 8.6 and Figure 8.7 in the blending book

When you click on the link above, you get a graphic editor to create and change curves of the blending splines type. The user interface is a menu at the top right and using the mouse as follows:

• With the left mouse button you move both knots and the "cubes" (that represent control curves).
• Pushing down the right mouse button you rotate the "cubes"  with the wheel.
• Pushing down the left mouse button you scale the "cubes"  with the wheel.
• If you hold down the Ctrl button on the keyboard, you can select "cubes" with the left mouse button.
Several "cubes" can be selected and they can also be deselected with the same mouse button. If you hold the mouse over one of the selected "cubes" you can move, rotate or scale all the selected "cubes" at the same time. Note that the Ctrl button must be held down all the times.

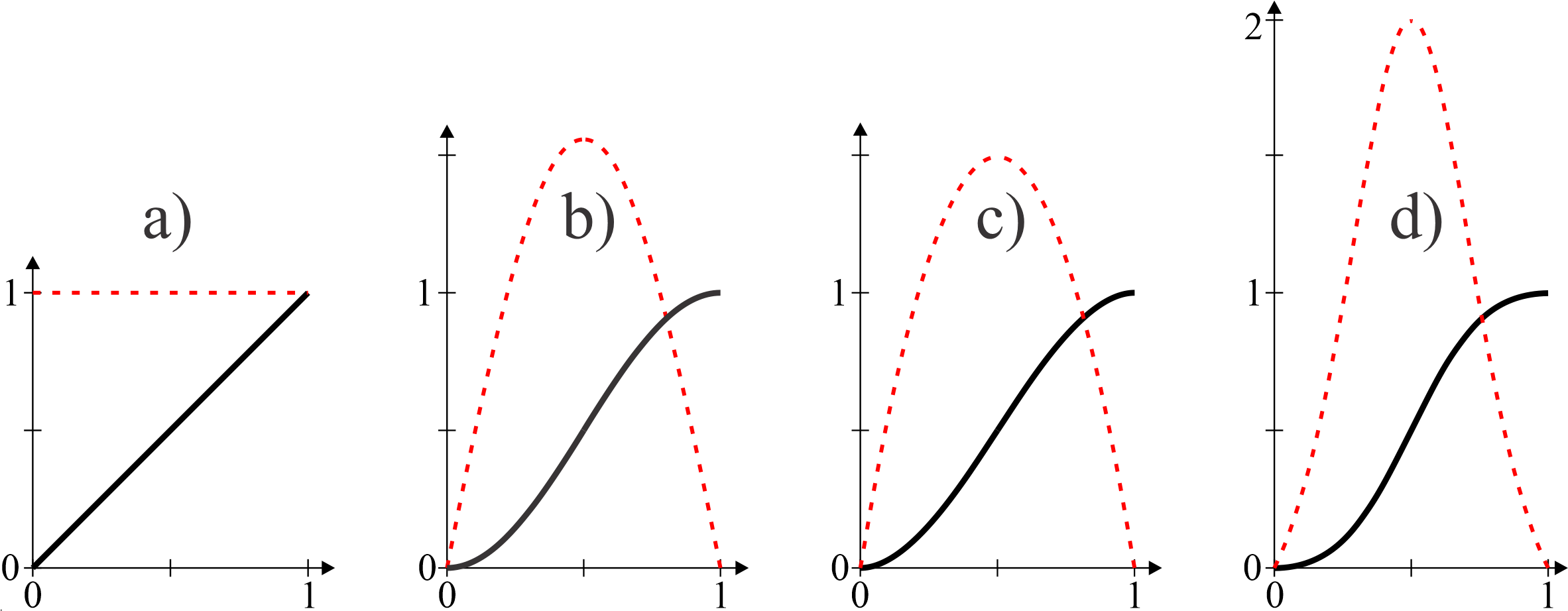
B functions are used for blending. Four B functions are plotted, as well as their derivatives (dashed red).

we have:    a) \(B(t)=t\),   b) \(B(t)=\frac{1}{2}- \frac{1}{2}\cos \pi t \),   c) \(B(t)=3t^2-2t^3\) and d) \(B(t)=\frac{t^2}{(1-t)^2 + t^2}\)

The plots is from Figure 7.1. B-functions are described in chapter 7 in the blending book.

Blending-splines formula is:   \( c(t) =  ( 1-B\circ w_{1,i}(t)  \quad  B\circ w_{1,i}(t) )  \begin{pmatrix} c_{i-1}(t) \\ c_{i}(t) \end{pmatrix}  \),  when \(t \in [t_i, t_{i+1})\).    See expression (8.7) page 152, chapter 8 in the book.